neka je 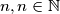 , te
, te 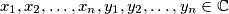
postoji li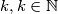 , takav da se iz jednakosti
, takav da se iz jednakosti 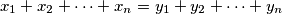
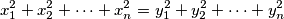

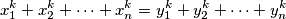
moze zakljuciti da su " -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.
dodatno, postoji li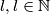 takav da se za proizvoljnih
takav da se za proizvoljnih  brojeva
brojeva 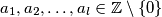 , takvih da
, takvih da 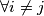 vrijedi
vrijedi 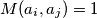 te odgovarajucih jednakosti
te odgovarajucih jednakosti
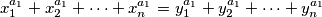
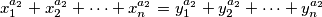

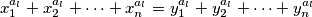
moze zakljuciti da su " -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.
takoder, uz pretpostavku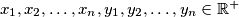 , smijemo li uzeti
, smijemo li uzeti 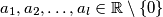 ?
?
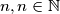 , te
, te 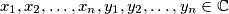
postoji li
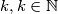 , takav da se iz jednakosti
, takav da se iz jednakosti 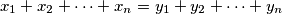
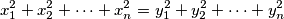

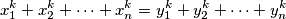
moze zakljuciti da su "
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.dodatno, postoji li
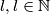 takav da se za proizvoljnih
takav da se za proizvoljnih  brojeva
brojeva 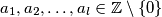 , takvih da
, takvih da 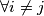 vrijedi
vrijedi 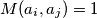 te odgovarajucih jednakosti
te odgovarajucih jednakosti 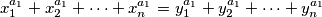
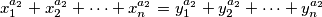

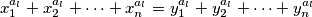
moze zakljuciti da su "
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.takoder, uz pretpostavku
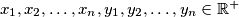 , smijemo li uzeti
, smijemo li uzeti 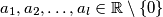 ?
?  Školjka
Školjka