Dan je raznostraničan šiljastokutan trokut  . Neka je
. Neka je  sjecište vanjske simetrale kuta
sjecište vanjske simetrale kuta 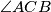 i pravca
i pravca  . Neka je
. Neka je  točka na kružnici opisanoj trokutu
točka na kružnici opisanoj trokutu  takva da je
takva da je 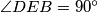 . Neka je
. Neka je  na istoj toj kružnici, tako da leži na manjem kružnom luku
na istoj toj kružnici, tako da leži na manjem kružnom luku  . Točka
. Točka  je sjecište pravaca
je sjecište pravaca 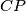 i
i 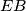 . Dokažite da je pravac
. Dokažite da je pravac 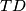 okomit na pravac
okomit na pravac  ako i samo ako vrijedi:
ako i samo ako vrijedi: 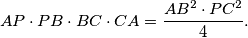
 . Neka je
. Neka je  sjecište vanjske simetrale kuta
sjecište vanjske simetrale kuta 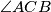 i pravca
i pravca  . Neka je
. Neka je  točka na kružnici opisanoj trokutu
točka na kružnici opisanoj trokutu  takva da je
takva da je 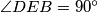 . Neka je
. Neka je  na istoj toj kružnici, tako da leži na manjem kružnom luku
na istoj toj kružnici, tako da leži na manjem kružnom luku  . Točka
. Točka  je sjecište pravaca
je sjecište pravaca 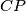 i
i 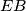 . Dokažite da je pravac
. Dokažite da je pravac 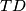 okomit na pravac
okomit na pravac  ako i samo ako vrijedi:
ako i samo ako vrijedi: 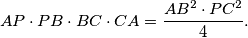
 Školjka
Školjka