Let
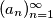
be a sequence of integers with
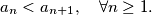
For all quadruple
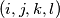
of indices such that
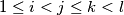
and
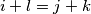
we have the inequality
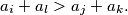
Determine the least possible value of
.
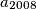
%V0
Let $(a_n)^{\infty}_{n=1}$ be a sequence of integers with $a_{n} < a_{n+1}, \quad \forall n \geq 1.$ For all quadruple $(i,j,k,l)$ of indices such that $1 \leq i < j \leq k < l$ and $i + l = j + k$ we have the inequality $a_{i} + a_{l} > a_{j} + a_{k}.$ Determine the least possible value of $a_{2008}$.
Školjka