Suppose that

is a cyclic quadrilateral and
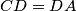
. Points

and

belong to the segments

and

respectively, and
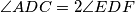
. Segments
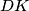
and
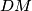
are height and median of triangle
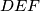
, respectively.

is the point symmetric to

with respect to

. Prove that the lines
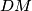
and
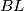
are parallel.
%V0
Suppose that $ABCD$ is a cyclic quadrilateral and $CD=DA$. Points $E$ and $F$ belong to the segments $AB$ and $BC$ respectively, and $\angle ADC=2\angle EDF$. Segments $DK$ and $DM$ are height and median of triangle $DEF$, respectively. $L$ is the point symmetric to $K$ with respect to $M$. Prove that the lines $DM$ and $BL$ are parallel.