We are given a cyclic quadrilateral

with a point

on the diagonal

such that
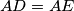
and
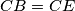
. Let

be the center of the circumcircle

of the triangle
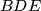
. The circle

intersects the line

in the points

and

. Prove that the lines
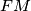
,

and

meet at one point.
%V0
We are given a cyclic quadrilateral $ABCD$ with a point $E$ on the diagonal $AC$ such that $AD=AE$ and $CB=CE$. Let $M$ be the center of the circumcircle $k$ of the triangle $BDE$. The circle $k$ intersects the line $AC$ in the points $E$ and $F$. Prove that the lines $FM$, $AD$ and $BC$ meet at one point.