In each vertex of a regular  -gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let
-gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let 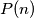 be the number of possible results of the shooting. Prove that for every positive integer
be the number of possible results of the shooting. Prove that for every positive integer 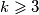 ,
, 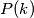 and
and 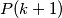 are relatively prime.
are relatively prime.
 -gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let
-gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let 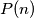 be the number of possible results of the shooting. Prove that for every positive integer
be the number of possible results of the shooting. Prove that for every positive integer 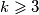 ,
, 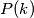 and
and 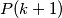 are relatively prime.
are relatively prime.  Školjka
Školjka