For a nonnegative integer

, define

to be the positive integer with decimal representation
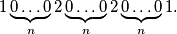
Prove that
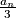
is always the sum of two positive perfect cubes but never the sum of two perfect squares.
%V0
For a nonnegative integer $n$, define $a_n$ to be the positive integer with decimal representation
$$1\underbrace{0\ldots0}_{n}2\underbrace{0\ldots0}_{n}2\underbrace{0\ldots0}_{n}1\mbox{.}$$
Prove that $\frac{a_n}{3}$ is always the sum of two positive perfect cubes but never the sum of two perfect squares.