In a plane the circles 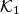 and
and 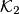 with centers
with centers 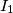 and
and 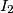 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 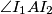 is obtuse. The tangent to
is obtuse. The tangent to 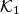 in
in  intersects
intersects 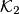 again in
again in  and the tangent to
and the tangent to 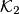 in
in  intersects
intersects 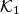 again in
again in  . Let
. Let 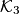 be the circumcircle of the triangle
be the circumcircle of the triangle  . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 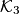 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 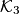 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line 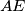 is perpendicular to
is perpendicular to 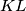 .
.
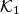 and
and 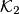 with centers
with centers 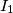 and
and 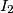 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 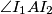 is obtuse. The tangent to
is obtuse. The tangent to 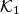 in
in  intersects
intersects 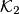 again in
again in  and the tangent to
and the tangent to 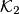 in
in  intersects
intersects 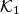 again in
again in  . Let
. Let 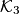 be the circumcircle of the triangle
be the circumcircle of the triangle  . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 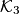 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 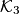 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line 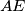 is perpendicular to
is perpendicular to 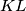 .
.  Školjka
Školjka