Let  be an integer. At a MEMO-like competition, there are
be an integer. At a MEMO-like competition, there are 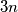 participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least
participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least 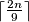 of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.
of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.
Note. is the smallest integer which is greater than or equal to
is the smallest integer which is greater than or equal to  .
.
 be an integer. At a MEMO-like competition, there are
be an integer. At a MEMO-like competition, there are 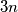 participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least
participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least 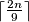 of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.
of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.Note.
 is the smallest integer which is greater than or equal to
is the smallest integer which is greater than or equal to  .
.  Školjka
Školjka