Let
and
be disjoint nonempty sets with
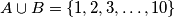
. Show that there exist elements
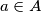
and
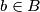
such that the number
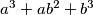
is divisible by
.
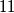
%V0
Let $A$ and $B$ be disjoint nonempty sets with $A \cup B = \{1, 2,3, \ldots, 10\}$. Show that there exist elements $a \in A$ and $b \in B$ such that the number $a^3 + ab^2 + b^3$ is divisible by $11$.
Školjka