Slični zadaci
Žicu duljine  m treba razrezati i od dobivenih dijelova napraviti jedan jednakostranični trokut i jedan kvadrat. Cijelu žicu treba iskoristiti. Odredi duljinu stranice trokuta i duljinu stranice kvadrata tako da zbroj površina trokuta i kvadrata bude što manji. Kolika je tada ukupna površina trokuta i kvadrata?
m treba razrezati i od dobivenih dijelova napraviti jedan jednakostranični trokut i jedan kvadrat. Cijelu žicu treba iskoristiti. Odredi duljinu stranice trokuta i duljinu stranice kvadrata tako da zbroj površina trokuta i kvadrata bude što manji. Kolika je tada ukupna površina trokuta i kvadrata?
 m treba razrezati i od dobivenih dijelova napraviti jedan jednakostranični trokut i jedan kvadrat. Cijelu žicu treba iskoristiti. Odredi duljinu stranice trokuta i duljinu stranice kvadrata tako da zbroj površina trokuta i kvadrata bude što manji. Kolika je tada ukupna površina trokuta i kvadrata?
m treba razrezati i od dobivenih dijelova napraviti jedan jednakostranični trokut i jedan kvadrat. Cijelu žicu treba iskoristiti. Odredi duljinu stranice trokuta i duljinu stranice kvadrata tako da zbroj površina trokuta i kvadrata bude što manji. Kolika je tada ukupna površina trokuta i kvadrata?  Školjka
Školjka  vrijedi
vrijedi 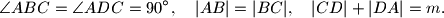
 .
. 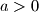 tako da površina lika omeđenog grafovima funkcija
tako da površina lika omeđenog grafovima funkcija 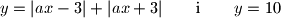 bude jednaka
bude jednaka  .
.  dane su točke
dane su točke 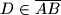 i
i 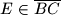 takve da je
takve da je 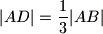 i
i 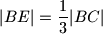 . Pravci
. Pravci  i
i  sijeku se u točki
sijeku se u točki  . Koliki je kut
. Koliki je kut 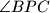 ?
?  i
i  presavijen je kao na slici.
presavijen je kao na slici.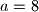 ,
, 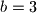 ,
, 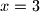 i
i 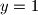 .
.  . Paralela sa stranicom
. Paralela sa stranicom  kroz
kroz  i
i  u točkama
u točkama  i
i  , paralela sa stranicom
, paralela sa stranicom  i
i  , a paralela sa stranicom
, a paralela sa stranicom  i
i 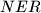 ,
, 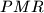 i
i 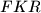 iznose redom
iznose redom 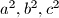 . Odredite površinu trokuta
. Odredite površinu trokuta