Imamo različite proste brojeve
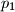
,
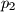
,

,
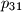
. Dokaži da, ako

dijeli sumu njihovih četvrtih potencija, među njima postoje

uzastopna prosta.
%V0
Imamo različite proste brojeve $p_1$, $p_2$, $\ldots$, $p_{31}$. Dokaži da, ako $30$ dijeli sumu njihovih četvrtih potencija, među njima postoje $3$ uzastopna prosta.