Skup
sastoji se od
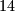
prirodnih brojeva. Pokažite da postoji
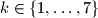
za koji je moguće naci
-člane disjunktne podskupove
i
skupa
tako da se sume
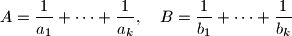
razlikuju za manje od
.
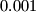
%V0
Skup $S$ sastoji se od $14$ prirodnih brojeva. Pokažite da postoji $k\in\{1, \ldots, 7\}$ za koji je moguće naci $k$-člane disjunktne podskupove $\{a_1, \ldots, a_k\}$ i $\{b_1, \ldots, b_k\}$ skupa $S$ tako da se sume
$$ A = \frac{1}{a_1} + \cdots + \frac{1}{a_k}, \quad B = \frac{1}{b_1} + \cdots + \frac{1}{b_k}$$ razlikuju za manje od $0.001$.
Školjka