Slični zadaci
Roko se šeće po ploči 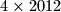 (
( retka,
retka, 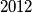 stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
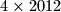 (
( retka,
retka, 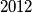 stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu? Initially, only the integer 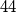 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 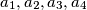 such that the arithmetic mean
such that the arithmetic mean 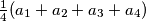 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After  steps we end up with
steps we end up with 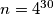 integers
integers 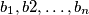 on the board. Prove that
on the board. Prove that 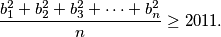
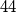 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 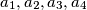 such that the arithmetic mean
such that the arithmetic mean 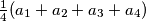 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After  steps we end up with
steps we end up with 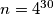 integers
integers 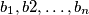 on the board. Prove that
on the board. Prove that 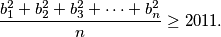
Kiki zamisli dvoznamenkasti broj, a Veki ga pokušava pogoditi. Ako Veki pogodi točan broj ili broj kojemu je jedna znamenka točna a druga se od točne razlikuje za 1 Kiki mu kaže "Toplo!", inače kaže "Hladno!". (npr. ako Kiki zamisli 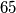 , za pogađane brojeve
, za pogađane brojeve 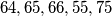 reći će "Toplo!", a za ostale "Hladno!")
reći će "Toplo!", a za ostale "Hladno!")
 Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od
Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od 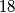 pokušaja.
pokušaja.
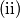 Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od
Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od 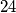 pokušaja.
pokušaja.
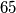 , za pogađane brojeve
, za pogađane brojeve 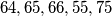 reći će "Toplo!", a za ostale "Hladno!")
reći će "Toplo!", a za ostale "Hladno!")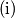 Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od
Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od 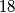 pokušaja.
pokušaja.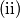 Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od
Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od 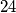 pokušaja.
pokušaja. Consider the two square matrices
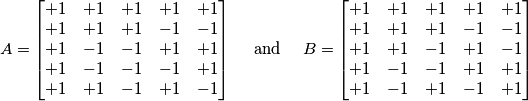
with entries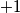 and
and  . The following operations will be called elementary:
. The following operations will be called elementary:
(1) Changing signs of all numbers in one row;
(2) Changing signs of all numbers in one column;
(3) Interchanging two rows (two rows exchange their positions);
(4) Interchanging two columns.
Prove that the matrix cannot be obtained from the matrix
cannot be obtained from the matrix  using these operations.
using these operations.
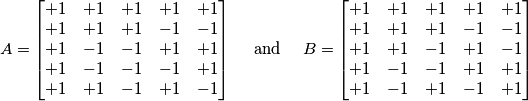
with entries
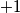 and
and  . The following operations will be called elementary:
. The following operations will be called elementary:(1) Changing signs of all numbers in one row;
(2) Changing signs of all numbers in one column;
(3) Interchanging two rows (two rows exchange their positions);
(4) Interchanging two columns.
Prove that the matrix
 cannot be obtained from the matrix
cannot be obtained from the matrix  using these operations.
using these operations.  Školjka
Školjka  sastoji se od
sastoji se od 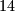 prirodnih brojeva. Pokažite da postoji
prirodnih brojeva. Pokažite da postoji 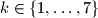 za koji je moguće naci
za koji je moguće naci  -člane disjunktne podskupove
-člane disjunktne podskupove  i
i  skupa
skupa 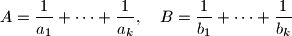 razlikuju za manje od
razlikuju za manje od 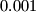 .
.  ,
,  i
i  novčića.
novčića. podskup skupa
podskup skupa 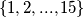 koji ne sadrži
koji ne sadrži  elementa čiji je umnožak potpun kvadrat. Odredi maksimalan broj elemenata skupa
elementa čiji je umnožak potpun kvadrat. Odredi maksimalan broj elemenata skupa