Neka su
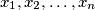
pozitivni realni brojevi takvi da je
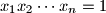
. Dokaži da vrijedi nejednakost:
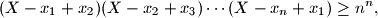
gdje je
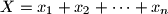
.
%V0
Neka su $x_1, x_2, \ldots, x_n$ pozitivni realni brojevi takvi da je $x_1x_2\cdots x_n=1$. Dokaži da vrijedi nejednakost: $$(X-x_1+x_2)(X-x_2+x_3)\cdots (X-x_n+x_1)\geq n^n\text{,}$$ gdje je $X=x_1+x_2+\cdots+x_n$.