Neka je
pravokutnik takav da vrijedi
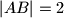
i
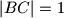
i neka su
,
,
,
točke na stranicama
,
,
,
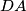
takve da je četverokut
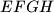
romb. Dokažite da tada za površinu
romba
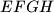
vrijedi
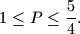
%V0
Neka je $ABCD$ pravokutnik takav da vrijedi $|AB| = 2$ i $|BC| = 1$ i neka su $E$, $F$, $G$, $H$ točke na stranicama $AB$, $BC$, $CD$, $DA$ takve da je četverokut $EFGH$ romb. Dokažite da tada za površinu $P$ romba $EFGH$ vrijedi $$ 1\leq P \leq \frac{5}{4}.$$
Školjka