Find all function
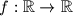
such that for all
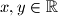
the following equality holds
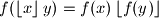
where
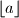
is greatest integer not greater than
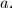
Proposed by Pierre Bornsztein, France
%V0
Find all function $f:\mathbb{R}\rightarrow\mathbb{R}$ such that for all $x,y\in\mathbb{R}$ the following equality holds $$f(\left\lfloor x\right\rfloor y)=f(x)\left\lfloor f(y)\right\rfloor$$
where $\left\lfloor a\right\rfloor$ is greatest integer not greater than $a.$
Proposed by Pierre Bornsztein, France