Let
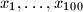
be nonnegative real numbers such that
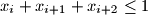
for all
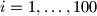
(we put
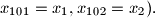
Find the maximal possible value of the sum
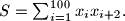
Proposed by Sergei Berlov, Ilya Bogdanov, Russia
%V0
Let $x_1, \ldots , x_{100}$ be nonnegative real numbers such that $x_i + x_{i+1} + x_{i+2} \leq 1$ for all $i = 1, \ldots , 100$ (we put $x_{101 } = x_1, x_{102} = x_2).$ Find the maximal possible value of the sum $S = \sum^{100}_{i=1} x_i x_{i+2}.$
Proposed by Sergei Berlov, Ilya Bogdanov, Russia