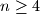
players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players
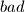
if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let
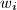
and
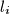
be respectively the number of wins and losses of the

-th player. Prove that
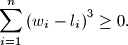
Proposed by Sung Yun Kim, South Korea
%V0
$n \geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players $bad$ if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_i$ and $l_i$ be respectively the number of wins and losses of the $i$-th player. Prove that
$$\sum^n_{i=1} \left(w_i - l_i\right)^3 \geq 0.$$
Proposed by Sung Yun Kim, South Korea
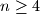 players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players
players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players 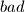 if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let
if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let 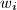 and
and 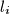 be respectively the number of wins and losses of the
be respectively the number of wins and losses of the  -th player. Prove that
-th player. Prove that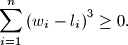
 Školjka
Školjka