Let 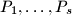 be arithmetic progressions of integers, the following conditions being satisfied:
be arithmetic progressions of integers, the following conditions being satisfied:
(i) each integer belongs to at least one of them;
(ii) each progression contains a number which does not belong to other progressions.
Denote by the least common multiple of the ratios of these progressions; let
the least common multiple of the ratios of these progressions; let 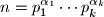 its prime factorization.
its prime factorization.
Prove that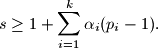
Proposed by Dierk Schleicher, Germany
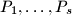 be arithmetic progressions of integers, the following conditions being satisfied:
be arithmetic progressions of integers, the following conditions being satisfied:(i) each integer belongs to at least one of them;
(ii) each progression contains a number which does not belong to other progressions.
Denote by
 the least common multiple of the ratios of these progressions; let
the least common multiple of the ratios of these progressions; let 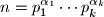 its prime factorization.
its prime factorization. Prove that
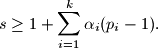
Proposed by Dierk Schleicher, Germany
 Školjka
Školjka