Three circular arcs 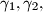 and
and 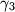 connect the points
connect the points  and
and 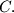 These arcs lie in the same half-plane defined by line
These arcs lie in the same half-plane defined by line  in such a way that arc
in such a way that arc 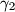 lies between the arcs
lies between the arcs 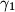 and
and 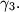 Point
Point  lies on the segment
lies on the segment 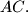 Let
Let 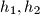 , and
, and 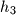 be three rays starting at
be three rays starting at 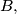 lying in the same half-plane,
lying in the same half-plane, 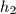 being between
being between 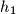 and
and 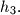 For
For 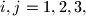 denote by
denote by 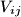 the point of intersection of
the point of intersection of 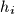 and
and 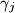 (see the Figure below). Denote by
(see the Figure below). Denote by 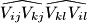 the curved quadrilateral, whose sides are the segments
the curved quadrilateral, whose sides are the segments 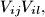
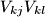 and arcs
and arcs 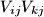 and
and 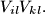 We say that this quadrilateral is
We say that this quadrilateral is 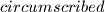 if there exists a circle touching these two segments and two arcs. Prove that if the curved quadrilaterals {{ INVALID LATEX }} are circumscribed, then the curved quadrilateral
if there exists a circle touching these two segments and two arcs. Prove that if the curved quadrilaterals {{ INVALID LATEX }} are circumscribed, then the curved quadrilateral 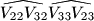 is circumscribed, too.
is circumscribed, too.
Proposed by Géza Kós, Hungary
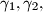 and
and 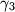 connect the points
connect the points  and
and 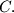 These arcs lie in the same half-plane defined by line
These arcs lie in the same half-plane defined by line  in such a way that arc
in such a way that arc 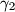 lies between the arcs
lies between the arcs 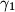 and
and 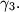 Point
Point  lies on the segment
lies on the segment 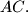 Let
Let 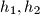 , and
, and 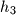 be three rays starting at
be three rays starting at 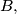 lying in the same half-plane,
lying in the same half-plane, 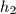 being between
being between 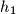 and
and 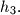 For
For 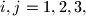 denote by
denote by 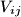 the point of intersection of
the point of intersection of 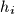 and
and 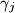 (see the Figure below). Denote by
(see the Figure below). Denote by 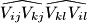 the curved quadrilateral, whose sides are the segments
the curved quadrilateral, whose sides are the segments 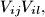
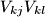 and arcs
and arcs 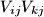 and
and 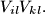 We say that this quadrilateral is
We say that this quadrilateral is 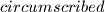 if there exists a circle touching these two segments and two arcs. Prove that if the curved quadrilaterals {{ INVALID LATEX }} are circumscribed, then the curved quadrilateral
if there exists a circle touching these two segments and two arcs. Prove that if the curved quadrilaterals {{ INVALID LATEX }} are circumscribed, then the curved quadrilateral 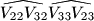 is circumscribed, too.
is circumscribed, too.Proposed by Géza Kós, Hungary
 Školjka
Školjka