Find the least positive integer
for which there exists a set
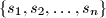
consisting of
distinct positive integers such that
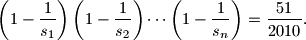
Proposed by Daniel Brown, Canada
%V0
Find the least positive integer $n$ for which there exists a set $\{s_1, s_2, \ldots , s_n\}$ consisting of $n$ distinct positive integers such that
$$\left( 1 - \frac{1}{s_1} \right) \left( 1 - \frac{1}{s_2} \right) \cdots \left( 1 - \frac{1}{s_n} \right) = \frac{51}{2010}.$$
Proposed by Daniel Brown, Canada
Školjka