Determine all sequences
of positive integers, such that for every positive integer
there exists an integer
with
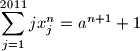
Proposed by Warut Suksompong, Thailand
%V0
Determine all sequences $(x_1,x_2,\ldots,x_{2011})$ of positive integers, such that for every positive integer $n$ there exists an integer $a$ with $$\sum^{2011}_{j=1} j x^n_j = a^{n+1} + 1$$
Proposed by Warut Suksompong, Thailand
Školjka