Let

be an acute triangle. Let

be a circle whose centre

lies on the side

. Suppose that

is tangent to

at
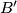
and

at
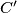
. Suppose also that the circumcentre

of triangle

lies on the shorter arc
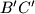
of

. Prove that the circumcircle of

and

meet at two points.
Proposed by Härmel Nestra, Estonia
%V0
Let $ABC$ be an acute triangle. Let $\omega$ be a circle whose centre $L$ lies on the side $BC$. Suppose that $\omega$ is tangent to $AB$ at $B'$ and $AC$ at $C'$. Suppose also that the circumcentre $O$ of triangle $ABC$ lies on the shorter arc $B'C'$ of $\omega$. Prove that the circumcircle of $ABC$ and $\omega$ meet at two points.
Proposed by Härmel Nestra, Estonia