For any integer
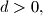
let
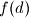
be the smallest possible integer that has exactly

positive divisors (so for example we have
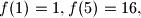
and
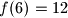
). Prove that for every integer
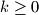
the number
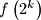
divides
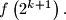
Proposed by Suhaimi Ramly, Malaysia
%V0
For any integer $d > 0,$ let $f(d)$ be the smallest possible integer that has exactly $d$ positive divisors (so for example we have $f(1)=1, f(5)=16,$ and $f(6)=12$). Prove that for every integer $k \geq 0$ the number $f\left(2^k\right)$ divides $f\left(2^{k+1}\right).$
Proposed by Suhaimi Ramly, Malaysia