Let
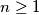
be an odd integer. Determine all functions

from the set of integers to itself, such that for all integers

and

the difference
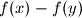
divides
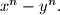
Proposed by Mihai Baluna, Romania
%V0
Let $n \geq 1$ be an odd integer. Determine all functions $f$ from the set of integers to itself, such that for all integers $x$ and $y$ the difference $f(x)-f(y)$ divides $x^n-y^n.$
Proposed by Mihai Baluna, Romania