For each positive integer
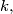
let
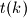
be the largest odd divisor of
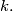
Determine all positive integers

for which there exists a positive integer
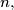
such that all the differences
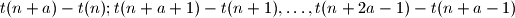
are divisible by 4.
Proposed by Gerhard Wöginger, Austria
%V0
For each positive integer $k,$ let $t(k)$ be the largest odd divisor of $k.$ Determine all positive integers $a$ for which there exists a positive integer $n,$ such that all the differences
$$t(n+a)-t(n); t(n+a+1)-t(n+1), \ldots, t(n+2a-1)-t(n+a-1)$$ are divisible by 4.
Proposed by Gerhard Wöginger, Austria