Let
be an odd prime number. For every integer
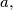
define the number
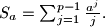
Let
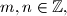
such that
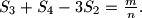
Prove that
divides
Proposed by Romeo Meštrović, Montenegro
%V0
Let $p$ be an odd prime number. For every integer $a,$ define the number $S_a = \sum^{p-1}_{j=1} \frac{a^j}{j}.$ Let $m,n \in \mathbb{Z},$ such that $S_3 + S_4 - 3S_2 = \frac{m}{n}.$ Prove that $p$ divides $m.$
Proposed by Romeo Meštrović, Montenegro
Školjka