Let

be the midpoint of the side

of a given triangle

. Let

and

be points on the sides

and

, respectively, such that
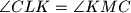
. Prove that the perpendiculars to the sides
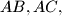
and

passing through
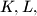
and

, respectively, are concurrent.
%V0
Let $K$ be the midpoint of the side $AB$ of a given triangle $ABC$. Let $L$ and $M$ be points on the sides $AC$ and $BC$, respectively, such that $\angle CLK = \angle KMC$. Prove that the perpendiculars to the sides $AB, AC,$ and $BC$ passing through $K,L,$ and $M$, respectively, are concurrent.