For any positive integer
let
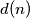
denote the number of positive divisors of
. Do there exist positive integers
and
, such that
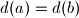
and
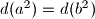
, but
?
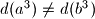
%V0
For any positive integer $n$ let $d(n)$ denote the number of positive divisors of $n$. Do there exist positive integers $a$ and $b$, such that $d(a)=d(b)$ and $d(a^2 ) = d(b^2 )$, but $d(a^3 ) \ne d(b^3 )$ ?
Školjka