Četverokut s vrhovima

,

,

i
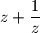
u kompleksnoj ravnini ima površinu
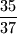
. Odredi najmanju moguću vrijednost izraza
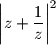
.
%V0
Četverokut s vrhovima $0$, $z$, $\displaystyle\frac 1z$ i $\displaystyle z+\frac 1z$ u kompleksnoj ravnini ima površinu $\displaystyle \frac{35}{37}$. Odredi najmanju moguću vrijednost izraza $\displaystyle \left| z+\frac 1z\right|^2$.