Zadan je niz

kao
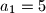
,
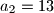
i
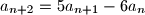
za

. Dokaži da za svaki član tog niza vrijedi
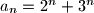
.
(

označava

-ti član niza. Ovdje su članovi niza definirani preko dva prethodna, tako je
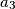
definiran kao

, a
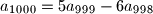
. Budući da jednakost vrijedi za svaki prirodni broj

, broj

je definiran za svaki prirodni broj

.)
%V0
Zadan je niz $a_n$ kao $a_1 = 5$, $a_2=13$ i $a_{n+2}=5a_{n+1}-6a_n$ za $n \in \mathbb{N}$. Dokaži da za svaki član tog niza vrijedi $a_n=2^n + 3^n$.
($a_n$ označava $n$-ti član niza. Ovdje su članovi niza definirani preko dva prethodna, tako je $a_3$ definiran kao $5a_2- 6a_1$, a $a_{1000}=5a_{999}-6a_{998}$. Budući da jednakost vrijedi za svaki prirodni broj $n$, broj $a_n$ je definiran za svaki prirodni broj $n$.)