Dokaži da je moguće popločati svaku
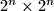
ploču, tako da se ostavi točno jedno prazno mjesto, koristeći samo domine oblika slova L sa jednakim krakovima:

.
%V0
Dokaži da je moguće popločati svaku $2^n \times 2^n$ ploču, tako da se ostavi točno jedno prazno mjesto, koristeći samo domine oblika slova L sa jednakim krakovima: $\setlength{\unitlength}{5pt}
\begin{picture}(2, 3)
\put(0, 0){\line(1, 0){1}}
\put(0, 0){\line(0, 1){2}}
\put(2, 2){\line(-1, 0){2}}
\put(2, 2){\line(0, -1){1}}
\put(1, 0){\line(0, 1){2}}
\put(0, 1){\line(1, 0){2}}
\end{picture}$.