Imamo

bijelih,

crvenih i

plavih žetona. U svakom koraku možemo uzeti po jedan sa neke dvije hrpe, i staviti jedan na treću hrpu. Dokaži da za fiksne
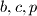
, kojim god redom radili ovo, ako dođemo do samo jednog žetona on će uvijek biti iste boje.
%V0
Imamo $b$ bijelih, $c$ crvenih i $p$ plavih žetona. U svakom koraku možemo uzeti po jedan sa neke dvije hrpe, i staviti jedan na treću hrpu. Dokaži da za fiksne $b,c,p$, kojim god redom radili ovo, ako dođemo do samo jednog žetona on će uvijek biti iste boje.