Zadane su funkcije
i
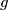
iz
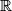
u
.
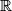
je bijekcija i za svaki realni
vrijedi:
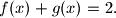
Pokaži da postoji točno jedan
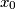
takav da je:
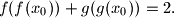
%V0
Zadane su funkcije $f$ i $g$ iz $\mathbb{R}$ u $\mathbb{R}$. $f$ je bijekcija i za svaki realni $x$ vrijedi: $$f(x) + g(x) = 2\text{.}$$
Pokaži da postoji točno jedan $x_0$ takav da je: $$f(f(x_0)) + g(g(x_0)) = 2\text{.}$$
Školjka