Neka je
jednakokračan trokut s
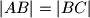
. Tangente na njegovu opisanu kružnicu u točkama
i
sijeku se u
. Pravac
siječe tu kružnicu još u točki
. Dokaži da
raspolavlja dužinu
.
%V0
Neka je $ABC$ jednakokračan trokut s $|AB| = |BC|$. Tangente na njegovu opisanu kružnicu u točkama $A$ i $B$ sijeku se u $D$. Pravac $CD$ siječe tu kružnicu još u točki $E$. Dokaži da $AE$ raspolavlja dužinu $BD$.
Školjka