
i

su kružnice s promjerima
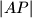
i
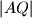
redom. One se sijeku još u točki

. Neka je
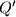
drugo sjecište kružnice

i pravca
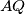
, a
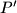
drugo sjecište kružnice

i pravca
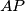
. Kružnica
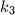
prolazi točkama
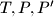
, a kružnicu
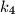
točkama
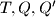
. Dokaži da pravac na kojem leži zajednička tetiva kružnica
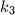
i
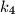
prolazi točkom

.
%V0
$k_1$ i $k_2$ su kružnice s promjerima $|AP|$ i $|AQ|$ redom. One se sijeku još u točki $T$. Neka je $Q'$ drugo sjecište kružnice $k_1$ i pravca $AQ$, a $P'$ drugo sjecište kružnice $k_2$ i pravca $AP$. Kružnica $k_3$ prolazi točkama $T, P, P'$, a kružnicu $k_4$ točkama $T, Q, Q'$. Dokaži da pravac na kojem leži zajednička tetiva kružnica $k_3$ i $k_4$ prolazi točkom $A$.