Dužina

je dulja stranica pravokutnika

. Okomica iz

na dijagonalu

siječe pravac

u točki

, a kružnica sa središtem u

koja prolazi kroz

siječe

u

. Dokažite da su
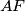
i

okomiti.
%V0
Dužina $AB$ je dulja stranica pravokutnika $ABCD$. Okomica iz $B$ na dijagonalu $AC$ siječe pravac $AD$ u točki $E$, a kružnica sa središtem u $A$ koja prolazi kroz $B$ siječe $CD$ u $F$. Dokažite da su $AF$ i $EF$ okomiti.