Neka je

trokut i
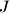
središte tom trokutu pripisane kružnice nasuprot vrhu

. Ta pripisana kružnica dodiruje

u

, a pravce

i

redom u

i

. Pravci
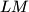
i
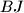
sijeku se u

, a
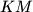
i
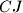
u

. Neka je

sjecište
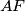
i

i neka je

sjecište
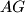
i

. Dokaži da je

polovište
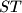
.
%V0
Neka je $ABC$ trokut i $J$ središte tom trokutu pripisane kružnice nasuprot vrhu $A$. Ta pripisana kružnica dodiruje $BC$ u $M$, a pravce $AB$ i $AC$ redom u $K$ i $L$. Pravci $LM$ i $BJ$ sijeku se u $F$, a $KM$ i $CJ$ u $G$. Neka je $S$ sjecište $AF$ i $BC$ i neka je $T$ sjecište $AG$ i $BC$. Dokaži da je $M$ polovište $ST$.