Neka je

šiljostokutan trokut s ortocentrom

i neka je
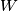
točka na

između

i

. Točke

i

su nožišta visina redom iz

i

.

je opisana kružnica
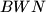
, a

točka takva da je
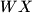
dijametar od

. Slično,

je opisana kružnica
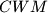
, a

je točka takva da je
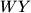
dijametar

. Dokažite da su

,

,

kolinearne.
%V0
Neka je $ABC$ šiljostokutan trokut s ortocentrom $H$ i neka je $W$ točka na $BC$ između $B$ i $C$. Točke $M$ i $N$ su nožišta visina redom iz $B$ i $C$. $k_1$ je opisana kružnica $BWN$, a $X$ točka takva da je $WX$ dijametar od $k_1$. Slično, $k_2$ je opisana kružnica $CWM$, a $Y$ je točka takva da je $WY$ dijametar $k_2$. Dokažite da su $X$, $Y$, $H$ kolinearne.