Let
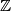
and
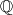
be the sets of integers and rationals respectively.
a) Does there exist a partition of
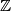
into three non-empty subsets
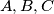
such that the sets
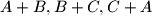
are disjoint?
b) Does there exist a partition of
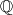
into three non-empty subsets
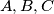
such that the sets
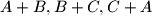
are disjoint?
Here
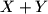
denotes the set
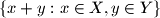
, for
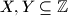
and for
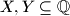
.
%V0
Let $\mathbb{Z}$ and $\mathbb{Q}$ be the sets of integers and rationals respectively.
a) Does there exist a partition of $\mathbb{Z}$ into three non-empty subsets $A,B,C$ such that the sets $A+B, B+C, C+A$ are disjoint?
b) Does there exist a partition of $\mathbb{Q}$ into three non-empty subsets $A,B,C$ such that the sets $A+B, B+C, C+A$ are disjoint?
Here $X+Y$ denotes the set $\{ x+y : x \in X, y \in Y \}$, for $X,Y \subseteq \mathbb{Z}$ and for $X,Y \subseteq \mathbb{Q}$.