Let
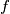
and
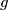
be two nonzero polynomials with integer coefficients and
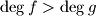
. Suppose that for infinitely many primes
the polynomial
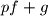
has a rational root. Prove that
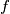
has a rational root.
%V0
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\deg f>\deg g$. Suppose that for infinitely many primes $p$ the polynomial $pf+g$ has a rational root. Prove that $f$ has a rational root.
Školjka