In a
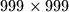
square table some cells are white and the remaining ones are red. Let

be the number of triples
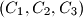
of cells, the first two in the same row and the last two in the same column, with
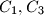
white and
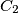
red. Find the maximum value

can attain.
%V0
In a $999 \times 999$ square table some cells are white and the remaining ones are red. Let $T$ be the number of triples $(C_1,C_2,C_3)$ of cells, the first two in the same row and the last two in the same column, with $C_1,C_3$ white and $C_2$ red. Find the maximum value $T$ can attain.