Let

be a cyclic quadrilateral whose diagonals

and

meet at

. The extensions of the sides

and

beyond

and

meet at

. Let

be the point such that
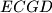
is a parallelogram, and let

be the image of

under reflection in

. Prove that
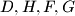
are concyclic.
%V0
Let $ABCD$ be a cyclic quadrilateral whose diagonals $AC$ and $BD$ meet at $E$. The extensions of the sides $AD$ and $BC$ beyond $A$ and $B$ meet at $F$. Let $G$ be the point such that $ECGD$ is a parallelogram, and let $H$ be the image of $E$ under reflection in $AD$. Prove that $D,H,F,G$ are concyclic.