For a nonnegative integer

define
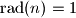
if
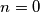
or
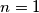
, and
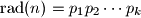
where
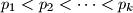
are all prime factors of

. Find all polynomials
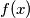
with nonnegative integer coefficients such that
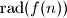
divides
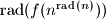
for every nonnegative integer

.
%V0
For a nonnegative integer $n$ define $\text{rad}(n)=1$ if $n=0$ or $n=1$, and $\text{rad}(n)=p_1p_2\cdots p_k$ where $p_1<p_2<\cdots <p_k$ are all prime factors of $n$. Find all polynomials $f(x)$ with nonnegative integer coefficients such that $\text{rad}(f(n))$ divides $\text{rad}(f(n^{\text{rad}(n)}))$ for every nonnegative integer $n$.