Find all positive integers

for which there exist non-negative integers
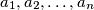
such that
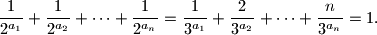
Proposed by Dusan Djukic, Serbia
%V0
Find all positive integers $n$ for which there exist non-negative integers $a_1, a_2, \ldots, a_n$ such that
$$\frac{1}{2^{a_1}} + \frac{1}{2^{a_2}} + \cdots + \frac{1}{2^{a_n}} = \frac{1}{3^{a_1}} + \frac{2}{3^{a_2}} + \cdots + \frac{n}{3^{a_n}} = 1\text{.}$$
Proposed by Dusan Djukic, Serbia