Zadane su 2 kružnice,  i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 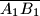 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 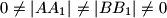 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 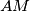 i
i 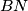 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 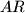 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 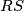 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
.
 i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 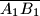 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 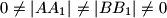 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 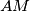 i
i 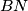 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 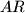 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 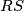 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
.  Školjka
Školjka