Olja zapiše

prirodnih brojeva
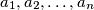
strogo manjih od
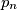
, gdje
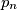
označava

-ti prosti broj. Oleg može odabrati dva (ne nužno različita) broja

i

te jednoga od njih zamijeniti produktom
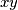
. Ako se pojave dva jednaka broja Oleg pobjeđuje. Može li Oleg garantirati pobjedu?
%V0
Olja zapiše $n$ prirodnih brojeva $a_1, a_2, \ldots, a_n$ strogo manjih od $p_n$, gdje $p_n$ označava $n$-ti prosti broj. Oleg može odabrati dva (ne nužno različita) broja $x$ i $y$ te jednoga od njih zamijeniti produktom $xy$. Ako se pojave dva jednaka broja Oleg pobjeđuje. Može li Oleg garantirati pobjedu?