U trokut

upisan je romb
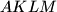
tako da točka

leži na

, točka

na

, a točka

na

. Ako je duljina stranice tog romba
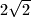
, površina trokuta
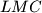
iznosi

, a površina trokuta
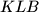
iznosi

, dokaži da je
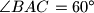
.
%V0
U trokut $ABC$ upisan je romb $AKLM$ tako da točka $K$ leži na $\overline{AB}$, točka $L$ na $\overline{BC}$, a točka $M$ na $\overline{CA}$. Ako je duljina stranice tog romba $2\sqrt{2}$, površina trokuta $LMC$ iznosi $3$, a površina trokuta $KLB$ iznosi $4$, dokaži da je $\angle BAC=60^\circ$.