U svaki vrh pravilnog dvanaesterokuta  upisan je ili broj
upisan je ili broj  ili broj
ili broj  . Na početku je u vrh
. Na početku je u vrh  upisan broj
upisan broj  , a u sve ostale vrhove broj
, a u sve ostale vrhove broj  . Dozvoljeno je istovremeno promijeniti predznak brojeva u bilo kojih šest uzastopnih vrhova tog dvanaesterokuta.
. Dozvoljeno je istovremeno promijeniti predznak brojeva u bilo kojih šest uzastopnih vrhova tog dvanaesterokuta.
Dokaži da ponavljanjem ovog postupka ne možemo postići da u vrh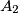 bude upisan broj
bude upisan broj  , a u sve ostale vrhove broj
, a u sve ostale vrhove broj  .
.
 upisan je ili broj
upisan je ili broj  ili broj
ili broj  . Na početku je u vrh
. Na početku je u vrh  upisan broj
upisan broj  , a u sve ostale vrhove broj
, a u sve ostale vrhove broj  . Dozvoljeno je istovremeno promijeniti predznak brojeva u bilo kojih šest uzastopnih vrhova tog dvanaesterokuta.
. Dozvoljeno je istovremeno promijeniti predznak brojeva u bilo kojih šest uzastopnih vrhova tog dvanaesterokuta.Dokaži da ponavljanjem ovog postupka ne možemo postići da u vrh
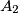 bude upisan broj
bude upisan broj  , a u sve ostale vrhove broj
, a u sve ostale vrhove broj  .
.  Školjka
Školjka